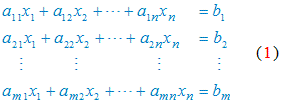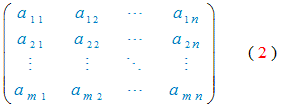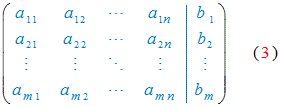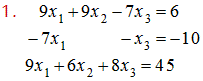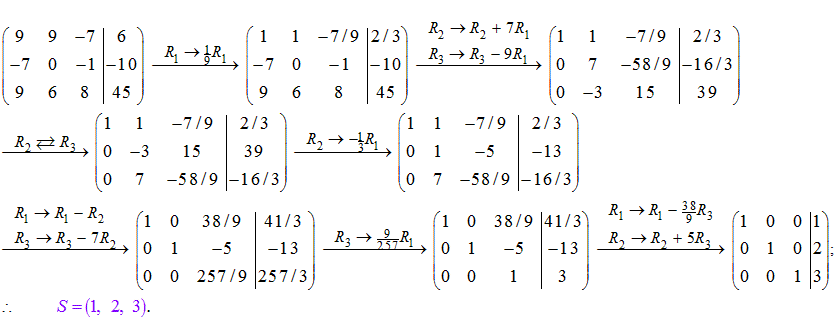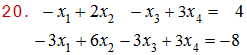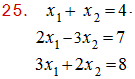Problemas 1.2
m ecuaciones con n incógnitas: Eliminación de Gauss-Jordan y gaussiana
 apuntes
apuntes
Apuntes
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
 Sistema de ecuaciones lineales
Sistema de ecuaciones lineales
Sistema de ecuaciones lineales. La forma general de un sistema de m ecuaciones lineales y n incógnitas es:
 Matriz
Matriz
Matriz. Una matriz es un arreglo rectangular de números distribuidos en forma ordenada en filas (renglones) y columnas. Cada uno de estos números es un elemento de la matriz. Los elementos de una matriz pueden ser números reales o complejos.
Una matriz con m renglones y n columnas se denomina matriz de m x n. El símbolo m x n se lee "m por n".
 Matriz de coefiecientes
Matriz de coefiecientes
Matriz de coeficientes. La matriz de coeficientes del sistema lineal (1) es la matriz:
 matriz aumentada
matriz aumentada
Matriz aumentada. El sistema lineal (1) se puede escribir utilizando la matriz aumentada
 Operaciones elementales por renglones
Operaciones elementales por renglones
Operaciones elementales por renglones. Las tres operaciones elementales por renglones aplicadas a la matriz aumentada que representa un sistema de ecuaciones lineales son:
i) Multiplicar (o dividir) un renglón por un número diferente de cero.
ii) Sumar un múltiplo de un renglón a otro renglón.
iii) Intercambiar dos renglones.
El proceso de aplicar las operaciones elementales por renglones para simplificar una matriz aumentada se llama reducción por renglones.
 Sistemas inconsistentes y consistentes
Sistemas inconsistentes y consistentes
Definición 1.2.1 Sistemas inconsistentes y consistentes.
Se dice que un sistema de ecuaciones lineales es inconsistente si no tiene solución. Si el sistema tiene al menos una solución se dice que es consistente.
 Forma escalonada reducida por renglones y pivote
Forma escalonada reducida por renglones y pivote
Definición 1.2.2 Forma escalonada reducida por renglones y pivote
Una matriz se encuentra en la forma escalonada reducida por renglones si se cumplen las
siguientes condiciones:
i) Todos los renglones (si los hay) cuyos elementos son todos cero aparecen en la parte inferior de la matriz.
ii) El primer número diferente de cero (comenzando por la izquierda) en cualquier renglón cuyos elementos no todos son cero es 1.
iii) Si dos renglones sucesivos tienen elementos distintos de cero, entonces el primer 1 en el renglón de abajo está más hacia la derecha que el primer 1 en el renglón de arriba.
iv) Cualquier columna que contiene el primer 1 en un renglón tiene ceros en el resto de sus elementos.
El primer número diferente de cero en un renglón (si lo hay) se llama pivote para ese renglón.
Nota. La condición iii) se puede reescribir como “el pivote en cualquier renglón está a la derecha del pivote del renglón anterior”.
 forma escalonada por renglones
forma escalonada por renglones
Definición 1.2.3 Forma escalonada por renglones
Una matriz está en la forma escalonada por renglones si se cumplen las condiciones i), ii) y iii) de la Definición 1.2.2.
 Eliminación de Gauss-Jordan
Eliminación de Gauss-Jordan
Eliminación de Gauss-Jordan. La eliminación de Gauss-Jordan es el proceso de resolución de un sistema de ecuaciones lineales mediante la reducción por renglones de la matriz aumentada asociada a la forma escalonada reducida por renglones.
 Eliminación Gaussiana
Eliminación Gaussiana
Eliminación Gaussiana. La eliminación gaussiana es el proceso de resolver un sistema de ecuaciones al reducir por renglones la matriz aumentada a la forma escalonada por renglones y utilizando la sustitución hacia atrás.
 Procedimiento
Procedimiento
Procedimiento para resolver un sistema de ecuaciones lineales
Para resolver un sistema de ecuaciones lineales aplicando operaciones elementales por renglones a la matriz aumentada asociada con el sistema, se procede como sigue:
1. Se escriben los coeficientes de las ecuaciones en una matriz aumentada
2. Se reduce la matriz a la forma escalonada reducida efectuando las operaciones elementales de renglón pertinentes (reducción por renglones)
3. Se deduce el valor numérico de cada incógnita
 Enunciados
Enunciados
Enunciados
En los problemas del 1 al 27 utilice el método de eliminación de Gauss-Jordan para encontrar, si existen, todas las soluciones de los sistemas dados:
En los problemas 28 a 39 determine si la matriz dada se encuentra en la forma escalonada por renglones (pero no en la forma escalonada reducida por renglones), en la forma escalonada reducida por renglones o en ninguna de las dos.
En los problemas 40 a 48 utilice las operaciones elementales con renglones para reducir las matrices dadas a la forma escalonada por renglones y a la forma escalonada reducida por renglones.
 Soluciones
Soluciones
Soluciones
 1
1
Solución- Juan Beltrán:
Escribimos el sistema como una matriz aumentada de coeficientes. Simplificamos la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada reducida; y se deduce la solución::
 2
2
Solución- Juan Beltrán:
Escribimos el sistema como una matriz aumentada de coeficientes. Simplificamos la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada reducida; y se deduce la solución::
 7
7
Solución- Juan Beltrán:
Se escribe el sistema como una matriz aumentada de coeficientes. Se simplifica la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada reducida; y se deduce la solución:
 10
10
Solución- Juan Beltrán:
Escribimos el sistema como una matriz aumentada de coeficientes. Simplificamos la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada reducida; y se deduce la solución::
 13
13
Solución- Juan Beltrán:
Escribimos el sistema como una matriz aumentada de coeficientes. Simplificamos la matriz efectuando operaciones elementales de renglón (reducción por renglones):
 15
15
Solución- Juan Beltrán:
Se escribe el sistema como una matriz aumentada de coeficientes. Se simplifica la matriz efectuando operaciones elementales de renglón (reducción por renglones); y se deduce la solución:
 17
17
Solución- Juan Beltrán:
Se escribe el sistema como una matriz aumentada de coeficientes. Se simplifica la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada reducida; y se deduce la solución:
 20
20
Solución- Juan Beltrán:
Se escribe el sistema como una matriz aumentada de coeficientes. Se simplifica la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada reducida; y se deduce la solución:
 23
23
Solución- Juan Beltrán:
Se escribe el sistema como una matriz aumentada de coeficientes. Se simplifica la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada; y se deduce la solución:
Solución- Juan Beltrán:
Se escribe el sistema como una matriz aumentada de coeficientes. Se simplifica la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada; y se deduce la solución:
 27
27
Solución- Juan Beltrán:
Se escribe el sistema como una matriz aumentada de coeficientes. Se simplifica la matriz efectuando operaciones elementales de renglón (reducción por renglones) llevándola a la forma escalonada reducida; y se deduce la solución:
En los problemas 28 a 39 determine si la matriz dada se encuentra en la forma escalonada por renglones (pero no en la forma escalonada reducida por renglones), en la forma escalonada reducida por renglones o en ninguna de las dos.
 28
28
 31
31
 35
35
 38
38
En los problemas 40 a 48 utilice las operaciones elementales con renglones para reducir las matrices dadas a la forma escalonada por renglones y a la forma escalonada reducida por renglones.
 40
40
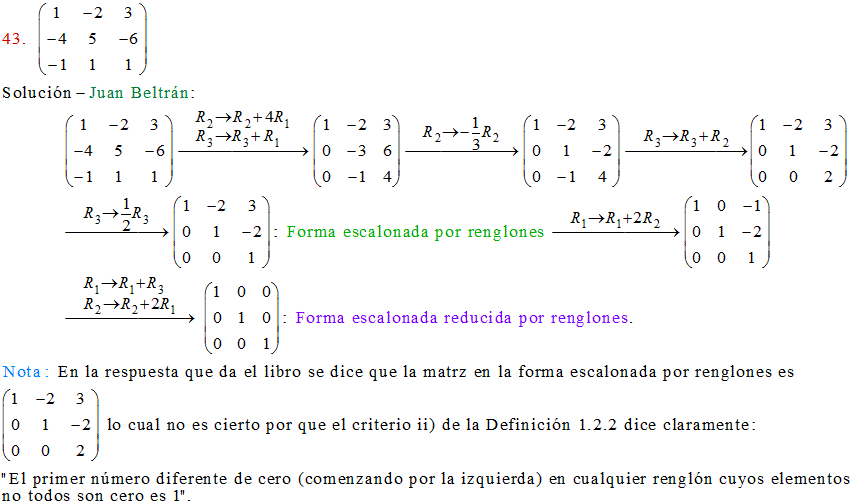
 43
43
 47
47
 48
48
 49
49
 51
51
 55
55
Lista de los Problemas del álgebra lineal (Ed. 7) de Stanley Grossman